关于 “许多博客中,给出的动态开点线段树 空间复杂度不够精确“ 的问题。
前言
10.25晚,在做codeforces round751 div2时,卡在了D题。
正好little_sun同学有事找我,我就把这道题丢了过去,然后他迅速给了个 线段树优化建图 的做法。
10.26下午的摸鱼课,我就来先学学前置算法 · 动态开点线段树了。
动态开点线段树
动态开点线段树的核心思想,就是通过 动态开点,来 节约大量的空间。
同时,它也是线段树优化建图等算法的前置技能,或者说技巧。
2021.10.29更正:线段树优化建图 不需要 动态开点线段树
如果你还不了解 动态开点线段树,可以参考 动态开点线段树
比如在 LuoguP1908逆序对 这道题中,我们可以用动态开点线段树来直接处理 [1,1e9] 的数据。
但是我根据博客教程写了一发,结果当场MLE。
参考题解,题解中把 最大空间 $O(nlogm)$ 直接缩小成了 $O(n * 14)$。
这就令人百思不得其解,翻遍整道题的题解也没有找到合适的解释。
在经过试验后,我发现网络上 大部分博客 的动态开点线段树的空间复杂度 存在着不精确,实际空间复杂度应该小于 $O(nlogm)$
结论
假设
动态开点线段树 的 区间长度为 $v$;
在操作时,总共修改 $n$ 次;
结论
总开点次数 $\large sum \leq 2^{log_2^n+log_2^{ln^2}}+n*(log_2^{\ \frac{v}{n}}+log_2^{ln^2})$
空间复杂度 即 $O(sum)$
正文
不精确的结论
首先,为什么大部分博客给出的空间复杂度上界为 $O(nlogv)$ ?
假设有 $n$ 次操作,每次操作最多能访问 $logv$ 个节点(这是线段树的基本结论)
根据乘法原理,我们很直观地得到了:一次运行中,线段树最多访问 $nlogv$ 个节点。
我们只创建访问到的节点,所以动态开点线段树的空间复杂度自然而然的就为 $O(nlogv)$
问题所在
看到这里,其实 所谓的不精确 就已经呼之欲出了。
在每次操作时,线段树的前几层的节点都已经创建完毕,无需再创建。
换句话说,每次操作访问到的 $logv$ 个节点,不一定都需要创建新点。
推导
先设一下算法中的 常量
- $v: 线段树的区间长度$
- $n: 总操作次数$
而既然误差在那些重复访问的点,我们可以假设 变量
- $k: 在算法结束时,前k层的节点已经全部创建完毕$
- 注意,这里的 $k$ 不一定为正整数,可能为实数
- 即 $k \in [0, logv+1]$
这里的假设或许不一定能得到最优解,我们先不深入讨论。
根据以上变量,我们能直观的得到一个更精确的开点次数
- $sum = (2^k-1)+n*(log_2^v-k)$
- $(2^k-1): 前k层创建的节点$
- $n*(log_2^v-k): 每次操作中,新创建的节点$
设 函数 $f(k) = (2^k-1)+n*(log_2^v-k), k \in [0, logv+1]$,则
$f’(k)=2^k*ln_2-n$,且显然,$f’(k)$ 单调递增
设存在 $f’(k_0)=0$,得到
$k_0 = log_2^n - log2^{ln^2}$
当 $k \in [0, k_0)$ 时,$f(k)$ 递减
当 $k \in (k_0, logv+1)$ 时,$f(k)$ 递增,得
$ f(k)\geq f(k_0)=2^{log_2^n+log_2^{ln^2}}+n*(log_2^{\ \frac{v}{n}}+log_2^{ln^2})$
即 总开点次数 $sum \leq 2^{log_2^n+log_2^{ln^2}}+n*(log_2^{\ \frac{v}{n}}+log_2^{ln^2})$
检验
以 LuoguP1908 为例。
$ n \leq 5e5,v \leq 1e9$
普通线段树 空间复杂度 $O(4 * v)=4e9$
动态开点线段树 不精确的空间复杂度 $O(nlogv) = 15e6$
动态开点线段树 在上述结论下的空间复杂度 $O(sum) \leq 6.47e6$
而在我自己出的极限数据下,动态开点线段树,实际开点数量为 $6.43e6$
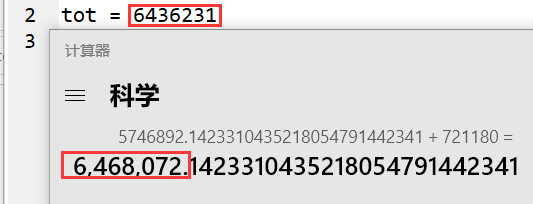
而如果你按照 $15e6$ 开数组空间,则无法通过这道题。
数组空间必须在 $10e6$ 内才能通过本题。
而有了精确的上界,你可以在开 $6.47e6$ 数组空间的情况下通过本题!
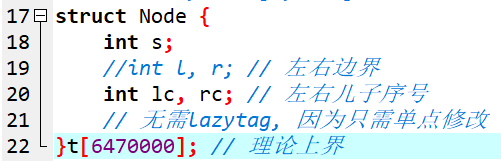

随便写写
推出来是很爽的!
但不知道有没有更准确的上界。
并且当前的上界值在实际写题时较难计算,
如果之后有机会的话,可以尝试用一个小常数来替换这一整串式子。
否则只能根据题目要求空间来开数组大小了。
下次看到这种解释不清楚的东西,还是要深究一下,说不定就有意想不到的收获呢!
OI is AWESOME!