1. 简介
本文实验了C++中一些内置函数的执行效率和精度的问题。
如果你也是算法竞赛选手的话,那么本文或许可以给你提供一些帮助。
CPU:i5-12400F
编译器:gcc.exe (x86_64-win32-seh-rev1, Built by MinGW-Builds project) 13.1.0
编译命令:g++ test.cpp 或 g++ test.cpp -O2
具体实验代码请见本文末尾
2. GCC编译器中的builtin系列函数
总所周知,GCC的builtin系列函数可以使用硬件进行加速,可以将暴力实现的 $O(log)$ 复杂度优化为 $O(1)$
但这些函数究竟有多快呢?
标准均为 1e8 次运算,单位均为 sec
builtin系列函数,参数默认为 无符号32位整数 无符号64为整数 ,请在末尾加上 ll,如 __builtin_popcountll()
2.1 __builtin_popcount
该函数用于求解一个无符号整数在二进制下的 $1$ 的个数
结论:能用popcount就要要用,效率差了10倍
序号
方法
1
2
3
4
5
均值
1
1e8次builtin popcount
0.146
0.153
0.157
0.147
0.164
0.153
2
1e8次builtin popcount(开O2)
0.144
0.142
0.144
0.154
0.144
0.145
3
1e8次O(log)的模拟
5.624
5.827
5.716
5.721
5.691
5.716
4
1e8次O(log)的模拟(开O2)
1.273
1.286
1.289
1.292
1.363
1.301
2.2 __builtin_clz
clz:count leading zeros
该函数用于求解一个无符号整数在二进制下的前导 $0$ 个数
2.3 __builtin_ctz
ctz:count trailing zeros
该函数用于求解一个无符号整数在二进制下的结尾 $0$ 个数
这里我们可以和经典的 lowbit(x) 来比较一下运行效率
#define lowbit(x) (x & -x)
结论:开O2的lowbit为什么跑得这么快,太离谱了(○´・д・)ノ
序号
方法
1
2
3
4
5
均值
1
1e8次builtin ctz和左移
0.171
0.172
0.170
0.171
0.176
0.173
2
1e8次builtin ctz和左移(开O2)
0.075
0.072
0.072
0.075
0.074
0.074
3
1e8次lowbit
0.169
0.172
0.174
0.174
0.177
0.173
4
1e8次lowbit(开O2)
0.025
0.024
0.025
0.026
0.025
0.025
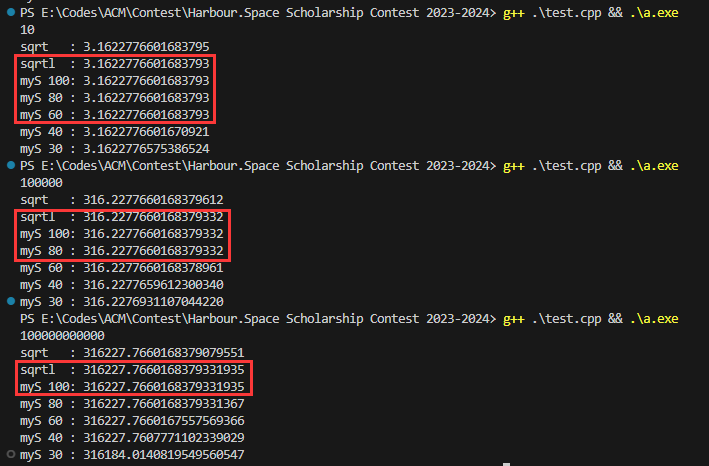
3. sqrt和sqrtl的精度问题
lovekdl老师说,sqrt精度很烂,写了必挂,所以我们队在对精度有要求的时候,就都用二分手动开根。
但这真的有必要吗?所以我来探究一下吧~(∠・ω< )⌒★!
注:输入及运算均为long double类型
注:众所周知,long double能表示的精度最多只到 1e-17,所以这里只输出16位
结论:sqrtl没有任何精度损失!不需要自己写二分!
数据如下。myS 是我自己实现的二分开根,后面的数字为二分次数
当然,这里为什么当输入数据为 100000 时,二分30次的效果反而差呢?
4. sqrt和二分的执行效率问题
序号
方法
1
2
3
4
5
均值
1
1e7次sqrtl
0.117
0.115
0.126
0.117
0.115
0.118
3
1e7次二分,每次二分50次
2.664
2.633
2.571
2.563
2.666
2.619
9. 实验代码
#define int long long void work () auto fm = clock (); int lim = 1e8 ; int cnt = 0 ; for (int i = 1 ; i <= lim; i++) { int x = i; while (x) { if (x & 1 ) cnt++; x >>= 1 ; } } auto ed = clock (); cout << fixed << setprecision (3 ); cout << cnt << " | " ; cout << 1.0 * (ed - fm) / CLOCKS_PER_SEC << " sec" << endl; }
2.3 __builtin_ctz & lowbit
#define int long long #define lowbit(x) (x&-x) void work () auto fm = clock (); int lim = 1e10 ; int cnt = 0 ; for (int i = 1 ; i <= lim; i++) { cnt += lowbit (i); } auto ed = clock (); cout << fixed << setprecision (3 ); cout << cnt << " | " ; cout << 1.0 * (ed - fm) / CLOCKS_PER_SEC << " sec" << endl; }
typedef long double db;db mySqrt (db x, int t) { db l = 0 ; db r = x; for (int i = 1 ; i <= t; i++) { db md = (l + r) / 2.0L ; if (md * md <= x) l = md; else r = md; } return l; } void work () db x; cin >> x; cout << fixed << setprecision (16 ); cout << "sqrt : " << sqrt (((double )(x))) << endl; cout << "sqrtl : " << sqrtl (x) << endl; cout << "myS 100: " << mySqrt (x, 100 ) << endl; cout << "myS 80 : " << mySqrt (x, 80 ) << endl; cout << "myS 60 : " << mySqrt (x, 60 ) << endl; cout << "myS 40 : " << mySqrt (x, 40 ) << endl; cout << "myS 30 : " << mySqrt (x, 30 ) << endl; }
#define int long long typedef long double db;db mySqrt (db x, int t) { db l = 0 ; db r = x; for (int i = 1 ; i <= t; i++) { db md = (l + r) / 2.0L ; if (md * md <= x) l = md; else r = md; } return l; } void work () auto fm = clock (); int lim = 1e7 ; int cnt = 0 ; for (int i = 1 ; i <= lim; i++) { cnt += sqrtl (i); } auto ed = clock (); cout << fixed << setprecision (3 ); cout << cnt << " | " ; cout << 1.0 * (ed - fm) / CLOCKS_PER_SEC << " sec" << endl; }